!!!UPDATE!!!
Since this post is still getting a lot of views, some of you might be interested in the
outcomes of my experiments with the cross K-function. I used the function in 2 recent
papers. Links to the articles are found on the Publications page.

Juhász, L. and Hochmair, H. H. (2017). Where to catch ‘em all? – a geographic analysis
of Pokémon Go locations. Geo-spatial Information Science. 20 (3): pp. 241-251

Hochmair, H.H., Juhász, L., and Cvetojevic, S. (2018). Data Quality of Points of
Interest in Selected Mapping and Social Media Platforms. Kiefer P., Huang H., Van de
Weghe N., Raubal M. (Eds.) Progress in Location Based Services 2018. LBS 2018. 
Lecture Notes in Geoinformation and Cartography (pp. 293-313) Berlin: Springer.

One of the research papers I’ve submitted recently (yes, about Pokémons!) dealt with spatial point pattern analysis. Visually it seemed that two of my point sets prefer to cluster around each other, in other words I suspected that Pokéstops have a preference of being close to Pokémon Gyms. Check the map below to see what I mean. Pokémon locations (cyan dots) are all over the place as opposed to Pokéstops (orange) that almost exclusively appear to be in the proximity of gyms (red).

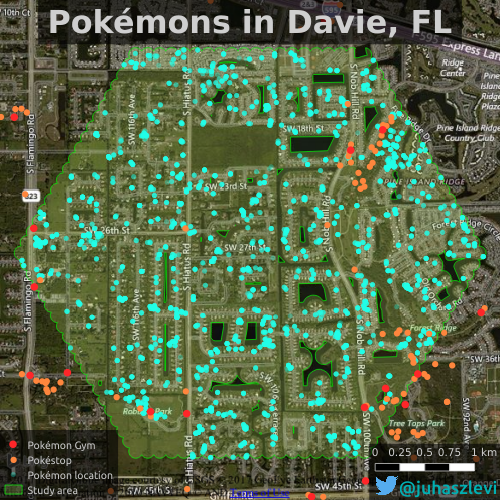
To confirm what’s obvious from the map, I used the bivariate version or Ripley’s K-function (a.k.a. the cross-K function) that can help us characterize two point patterns. As it turns out, it’s not as easy to interpret as I though it would be (at least with real world data) and I was trying to get my head around it for quite some time. As a result, I came up with a simple interactive visualization of this function to illustrate what it really means. If you’re anything like me and try to understand your stats instead of just reporting the results, you might want to read on more for some musings about the cross K-function.

Ripley’s K and cross-K functions

In spatial statistics, Ripley’s K-function can be used to characterize point patterns (i.e. if they’re clustered, dispersed or randomly distributed). Basically it tells you whether you observe more/less points within a given radius than what would be expected under complete spatial randomness. The bivariate version of the same function does the same for marked point patterns (or for two point patterns). It reports the number of type j events within a given radius of type i events. It is calculated as follows:

(see Dixon 2002 for details). Simply put, we’re inserting circles with growing radius on type i events (~controls) and check how many type j events (cases) are nearby. Theoretically, there could be two different cross K-functions but K_ij = K_ji therefore, it is enough to compute K_ij. If events are a result of a random spatial process (i.e. points are drawn from a homogeneous Poisson distribution), we can simplify the K function to K(r) = πr². This theoretical function represents complete spatial randomness and can be used to compare our observed cross-K function to.

 Making sense of the function

And now the fun part begins. First step is looking at the observed cross K pattern and the theoretical Poission K curve (under CSR). These two curves allow you to assess the relationship between type j (remember Pokéstops?) and i (gym) events. An observed cross K curve well above the theoretical K curve means that type j points prefer to cluster around type i points. In simple words (referring back to the Pokémon example) this scenario means that Pokéstops are attracted to Pokémon gyms. Or we can further tweak the words and say type j events are closer to type i events than it would be expected under complete spatial randomness. Either interpretation works. Similarly, if the observed cross K-function is below the the Poisson-K, type j events prefer to disadvantage type i events (~Pokéstops would be further from gyms). Unfortunately for the bivariate case of K function, it is not easy to test whether the deviation from the theoretical curve is meaningful or not (like if the the curves differ significantly) so in this step it’s enough to rely on your instincts. Just get a sense of the the observed pattern, keep in mind what would be expected under CSR and you can interpret your results easily.

Testing statistical significance

We were taught to report statistical significance as this is how we can support our findings. The original question I asked was whether Pokéstops and Pokémon Gyms are SIMILARLY clustered or not. Statistical inference of difference can be tested with a Monte Carlo simulation with random labeling. Namely, we can randomly assign points as type i and j (keeping the original rations) and compute the same cross K-function. The simulation mean and the established simulation envelopes tells us whether the observed between type pattern is statistically significant or not. An observed curve within the confidence envelopes means that no matter how we group your points into categories, the pattern we identified in the previous step (by checking on the observed and theoretical values) doesn’t change when randomly assigning events into categories.

Example patterns

Below is an interactive visualization of the these things that helped me understand how these functions works. I started off having 25 type j (blue) and 5 type i (red) events as a result of a random spatial process within a 10 unit radius circle. The observed cross K function (grey line) and the theoretical Poission K-function (red dashed line) are shown in the second plot. The third plot shows the results of a Monte Carlo simulation (99 steps) of random labeling of events (simulation mean – red dashed line; confidence envelope – yellow area). By clicking on the radio buttons, you can change the point pattern into a few predefined scenarios and assess how that affects the cross K function. It helped me a great deal to understand the principles. I hope that it will help you as well to make sense of the cross K function and you can use this tool to interpret your own results.

** Select a point pattern**

A simple interpretation of Point Pattern 2

Type i events (blue points) seem to cluster around type j events (red). It appears that the overall point pattern is clustered (could be confirmed with an univariate K-function). Calculating the cross K-function (2nd plot) reveals that there’s an interaction between types as the observed curve is above the Poission-curve (what would be expected under randomness). In other terms, it means blue points tend to be attracted to red points as we observe more blue points in the proximity of red ones than if their positions were random. For larger distances (> 4) the pattern is closer to random but that’s just the effect of their spatial distribution (the study area is small and using larger radius  eventually means selecting most of the points).

As for the Monte Carlo simulation, the grey line running close to the simulated mean would indicate that these two point patterns cluster similarly. However, we can even tell more! For shorter distances, it appears that blue points are even closer to red ones (i.e. observed cross K above the high simulation envelope) than it is the case  when randomly re-labeling them so their attraction is even stronger than expected.

To learn more about the cross K-function, check out this material:

Dixon, Philip M. 2002. “Ripley’s K function.” In Encyclopedia of Environmetrics 1796– 803. Wiley Online Library.

The computations and simulation steps in this post were conducted in R with the spatstat package. The visualization is D3.js. To reproduce this experiment, check out the data and code (even the visualization) on my GitHub.